LOF: Identifying Density-Based Local Outliers abstract。

解决的问题

之前的工作大多数研究将异常值视为二元属性，数据中的对象要么是异常值要么不是，在应用程序中情况更为复杂，并且为每一个对象分配一个异常值更有意义。

除此之外还有大量关于聚类算法的工作，从聚类算法的角度来看，离群值是不位于数据集聚类中的对象，通常称为噪声。聚类算法产生的噪声高度依赖于特定算法及其聚类参数。通常这些算法从全局的角度考虑异常值，这将会导致一些缺点。
本文针对此类缺点，提出 LOF 用于表征局部异常值。

以往关于离群点检测的研究大多是在统计学领域进行的，这些研究可以大致分为两类：

  • 基于分布的，问题是单变量和数据集潜在分布未知
  • 基于深度的，将数据点表示到 k 维空间，问题是在 k >= 4 时效率会降低

根据直觉的异常值定义：
defination of outlier

该定义中定义异常值为离群以至于怀疑是其他机制产生的。
Knorr 和 Ng 在对该定义进行了形式化：

defination of outlier formalization
当然以上定义是在全局层面，如下图所示，现实数据集中也存在着局部的异常值：
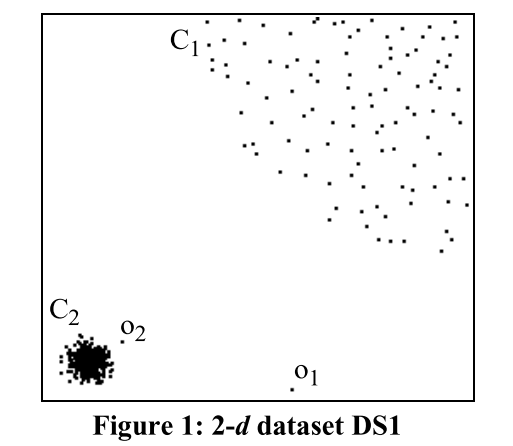
outliers

作者针对全局异常值定义的确定提出了局部异常值定义，关键点在于离群不是一个二元属性，并为每个对象制定了一个离群因子：

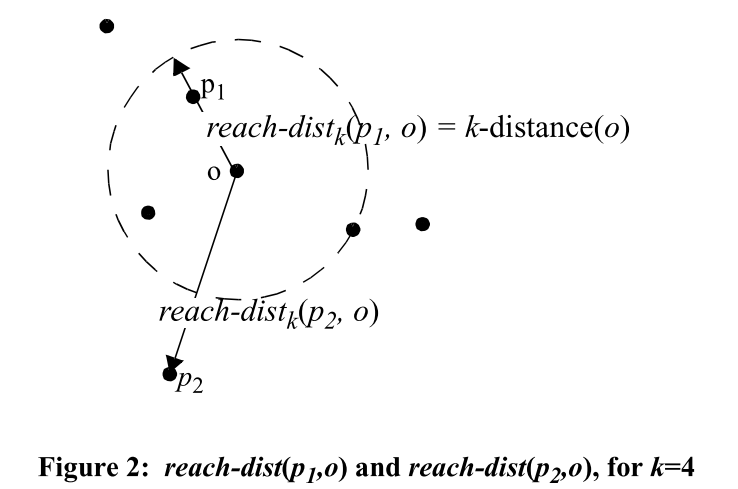
outliers
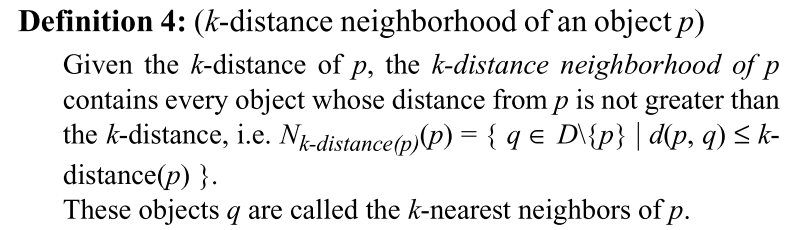
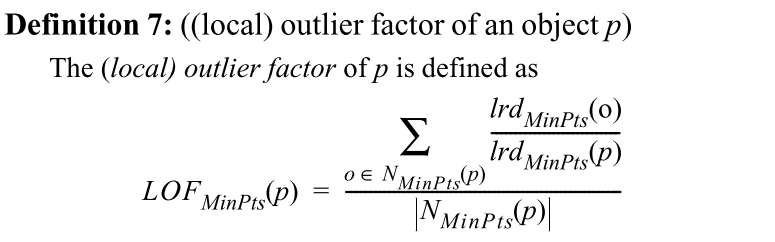
defination of outlier
defination of outlier
defination of outlier
defination of outlier
defination of outlier

LOF 的属性

  • 非离群值的LOF接近于1
  • 该LOF存在通用的上下界
  • 上下界是具有紧密性的，表现在非离群值趋近于1，离群值不接近1，但是其预测的LOF界限是严格的
  • 使用多集群重合的直接邻域边界，在上下边界失效时

讨论MinPts对LOF的影响

略

实验效果

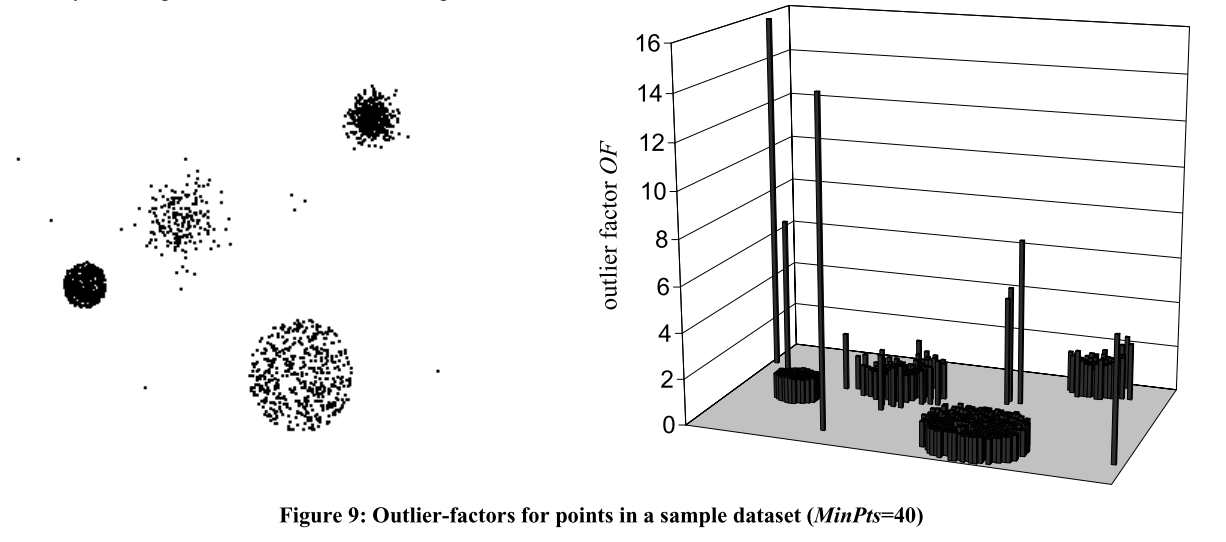
outliers